Index of Graph Theory
- 1. General
- 2. Implementation in Zeus-Framework
- 3. Usefull links to the graph theory
1. General
The Zeus-Framework provieds a collection of graph algorithmes. A graph is a general data structure for trees, lists, networks etc. Following list defines some specific expressions:
- Graph: A graph contains vertices and edges.
- Directed graph: The edges of the directed graph are pointing only in one direction.
- Weigthed graph: all edges are weighted
- Complete graph: all vertices are connected to each other.
- Cycle: Traversing the graph at least one vertice will be visited more than once (loop).
- Tree: A tree is a directed graph. Each vertice as one parent vertice, except the root vertice. The root vertice has no parent.
- Spanning tree: A tree is a sub graph containing a sub set of all edges.
- Isomorphism: A graph G1 is isomorph with G2 if there exists a complete mapping G1 = f(G2) and G2 = fc(G1)
- Complement: The complement graph contains all inverted edges off the original graph.
2. Implementation in Zeus-Framework
2.1 Classes of Zeus-Framework
There are 3 classes for graph implementation.
- TGraph: Heap class witch contains a graph
- TVertice: Defines a vertice of the graph
- TEdge: Defines an edge between two vertices.
2.2 Creating a undirected, weighted graph
The following example shows a undirected but weighted graph.

#include <zeusmath/System/Graph.h>
//Creates a undirected, weighted graph
TAutoPtr<TGraph> pGraph = new TGraph(false);
pGraph->addVertice(1);
pGraph->addVertice(2);
pGraph->addVertice(3);
pGraph->addVertice(4);
pGraph->addVertice(5);
pGraph->addVertice(6);
pGraph->addEdge(1,2, 6);
pGraph->addEdge(1,3, 1);
pGraph->addEdge(1,4, 5);
pGraph->addEdge(2,3, 5);
pGraph->addEdge(2,5, 3);
pGraph->addEdge(3,4, 5);
pGraph->addEdge(3,5, 6);
pGraph->addEdge(3,6, 4);
pGraph->addEdge(4,6, 2);
pGraph->addEdge(5,6, 6);
2.3 Creating a minimum-cost spanning tree
Out of a weighted graph we can create the minimum-cost spanning tree. It represents the cheapest network of this graph. Zeus-Framework implements the Prim algorithm to get this spanning tree.
Using the method getMinimumCostTree() returns a new graph representing the spanning tree. Optional we can tell the start vertice witch becomes the root node of the spanning tree.
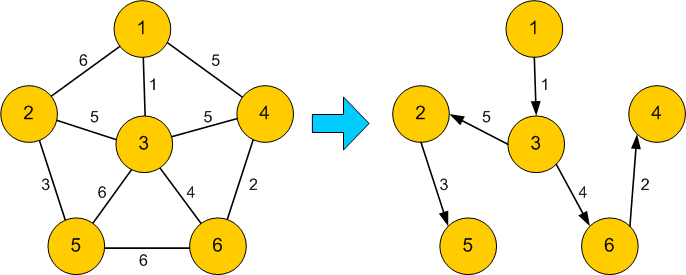
#include <zeusmath/System/Graph.h>
//Creates a undirected, weighted graph
TAutoPtr<TGraph> pGraph = new TGraph(false);
...
TAutoPtr<TGraph> pMinTree = NULL;
if (pGraph->getMinimumCostTree(1, pMinTree) == RET_NOERROR)
{
...
}
2.4 Cycle test
Directed graphs might have cycles. Cycles are endless loops while traversing the graph. On undirected graphs each edge is a cycle.
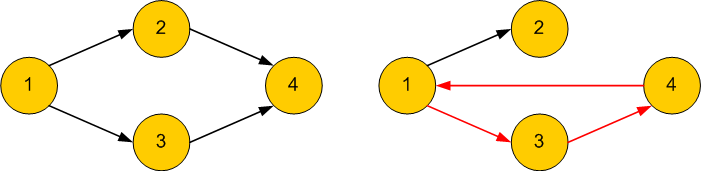
#include <zeusmath/System/Graph.h>
TAutoPtr<TGraph> pGraph = new TGraph(false);
...
if (pGraph->hasCycle())
{
...
}
2.5 Graph iterators
There are two ways how to iterate through a graph:
- Depth first search
- Breath first search
2.5.1 The depth first search
The depth first search iterates into the depth first. Following images shows how it works. The iteration step is shown inside the box. To the right the return sequence is shown.

#include <zeusmath/System/Graph.h>
TAutoPtr<TGraph> pGraph = new TGraph(false);
...
TAutoPtr<TGraphIterator> pIt = pGraph->getDepthFirstIterator();
TAutoPtr<TVertice> pVertice = NULL;
while(pIt->getNextVertice(pVertice) == RET_NOERROR)
{
...
}
2.5.2 The breath first search
The breath first search goes into the breath first, witch means it visits all vertices of level 1, all of level 2 etc.

#include <zeusmath/System/Graph.h>
TAutoPtr<TGraph> pGraph = new TGraph(false);
...
TAutoPtr<TGraphIterator> pIt = pGraph->getBreathFirstIterator();
TAutoPtr<TVertice> pVertice = NULL;
while(pIt->getNextVertice(pVertice) == RET_NOERROR)
{
...
}
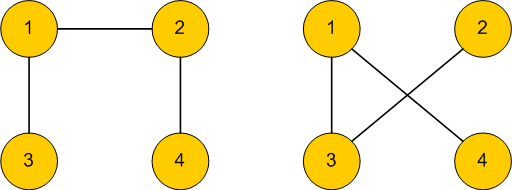
2.6 Isomorphism
Isomorphism is a mathematical expression for bijective mappings. For graph theorie we are faced with mappings if we get two "different looking" graphs and we want to know if they are actualy have the same structure. The following illustration shows an isomorph graph with the mapping
1 --> 1
2 --> 3
3 --> 4
4 --> 2Also the mapping
1 --> 3
2 --> 1
3 --> 2
4 --> 4is a valid mapping.
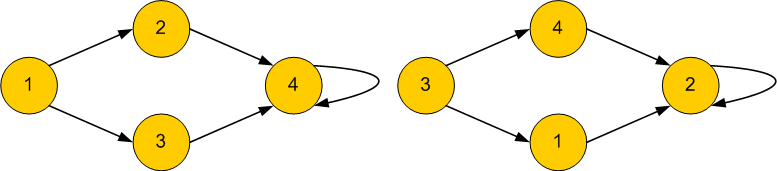
The next illustration shows a directed graph mapping. To check if a directed graph is isomorph with an other, we have to check to edge direction as well. And for weighted edges we have to match the weights too.
This is not an isomorph graph, since the edge E(V2,V2) can not be matched with the edge E(V3, V3).
2.6.1 Isomorphism algorithm
The problem of solving the isomorphism is NP (nondeterminisic polynominal). This means there exists no algorithm witch solves the problem in polynominal time so far, but it's not even proved, that there exists no such polynominal algorithm. Therefore The Zeus-Framework uses a algorthm having an exponential time complexity
The following lines describe the algorithm implemented in Zeus-Framework as pseudo code. The first part makes sure also islands of vertices are mapped. For each vertice of Graph G1 we try to find a corresponding match of Graph G2:
getIsomorphicMatches:= function(G1, G2, Matches)
begin
if ¦G1::V¦ = ¦G2::V¦ and
¦G1::E¦ = ¦G2::E¦ and
G1.isDirected = G2.isDirected then
begin
for each V1 in G1 do
for each V2 in G2 do
if !isMarked(V1) and !isMarked(V2) then
matchSubgraph(V1, V2, Matches)
end
end
end
end
//All vertices must be matched
if ¦Matches¦ = ¦G1:V¦ then
getIsomorphicMatches:= true
else
clear(Matches);
getIsomorphicMatches:= false
end
end
The matchSubgraph() routine tries to find now a correponding match starting from the vertice G1::V1 and G2::V2. As long as there is no contradiction in our matching process, we continue. If we find a contradiction we have to backtrack and try an other way. Once we could match all connected neighbours of the vertice G1::V1 with all connected neighbours of vertice G2::V2, we have found a connected! graph G1' matching the connected graph G2'. Note that G1' might be a part of the graph G1. But since our first routine getIsomorphicMatches() continues for all not yet marked vertices, we try to match all unconnected graphs G1'' also.
matchSubgraph:= function(V1, V2, Matches)
begin
contradiction:= true;
if edgeCount(V1) = edgeCount(V2) then
begin
//V1 and V2 already matched
if contains(Matches, pair(V1,V2)) then
contradiction:= false
//No edges try this match
else if (getEdgeCount(V1) = 0) then
mark(V1); mark(V2);
add(Matches, pair(V1, V2));
contradiction:= false
//Check if V1 and V2 are not yet matched with some
//other vertices
else if !isMarked(V1) and !isMarked(V2) then
temp_marks:= marks;
temp_Matches:= Matches;
mark(V1); mark(V2);
add(Matches, pair(V1, V2));
while contradiction and p = nextpermutation(V2.neighbours) do
contradiction:= false;
while V1_n = nextneighbour(V1) and
V2_n = next_item(p) and
!contradiction do
//Check if the weight of the edge matches
if edge_weight(V1, V1_n) = edge_weight(V2, V2_n) then
contradiction:=
contradiction & matchSubgraph(V1_n, V2_n, Matches)
else
contradiction:= true
end
end
end
//Undo changes of marks and Matches
if contradiction = true then
marks:= temp_marks;
Matches:= temp_Matches
end
end
end
matchSubgraph:= contradiction;
end
2.6.2 Checking isomorphism with Zeus-Framework
The TGraph-class implements the mapping of graphs. There are two kinds of checks. The first check looks for a exact match of two graphs (1 --> 1, 2 --> 2, ...). The second applies the for isomorphism checks. Be aware that the problem of isomorphism checks is NP, witch means the worst case is exponentialy.
Exact match:
TAutoPtr<TGraph> pGraph1 = new TGraph(false);
TAutoPtr<TGraph> pGraph2 = new TGraph(false);
...
if (ptrGraph1->equals(*ptrGraph2, false))
{
//graphs match exactly
}
Isomorphism match:
TAutoPtr<TGraph> pGraph1 = new TGraph(false);
TAutoPtr<TGraph> pGraph2 = new TGraph(false);
...
if (ptrGraph1->equals(*ptrGraph2, true))
{
//graphs are isomorph
}
The TGraph class implements also a routine to return the matches:
TAutoPtr<TGraph> pGraph1 = new TGraph(false);
TAutoPtr<TGraph> pGraph2 = new TGraph(false);
...
TSet<TPair<Uint, Uint> > setMatches;
if (ptrGraph1->getIsomorphicMatches(*ptrGraph2, setMatches)
== RET_NOERROR)
{
//set contains all matched pairs of vertices
}
2.7 Complementary Graph
The complementary graph is an inversion of the edges. In Zeus-Framework we consider two kinds of graphs, the undirected and directed graphs. Lets look at the undirected graphs first.
2.7.1 Complement of undirected graphs
Let G=(V,E) be an undirected graph. An edge is a set of two vertices Ex={v1, v2}. Then the complementary graph Gc is defined as follows:
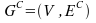
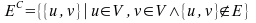

Never the less this is not quite complete. Since we are dealing with weighted edges, we have to consider the complement of the weights also. Edges for weighted graphes contain a set or vertices and the weight Ex=({u,v},w). For the complementary edges we use the following formula:
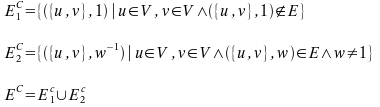

2.7.2 Complement of directed graphs
Let G=(V,E) be a directed graph. An edge is an ordered pair of vertices Ex=(v1, v2). Therefore the Edge Ey=(v2, v1) is not the same edge but the inverse. The complementary graph Gc is defined as follows:
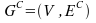
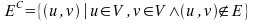

Again we are dealing with weighted edges. So we have to extend the definition as follows:
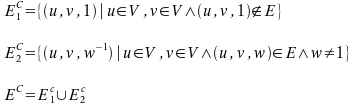

As we can see the only difference is the representation of an edge. The directed graphs have a stronger definition than undirected graphs. We can mapp an undirected graph G1 to an directed graph G2. For each edge {u,v} in G1 we create the edges (u,v) and (v,u).
2.7.2 Algorithm
Since the TGraph class handles directed and undirected, weighted and unweighted graphs in the same structure, the used algorithm can handle all the described variants (see above). The pseudo code function complement takes the set of vertices V and the set of edges E as input and returns the set of complement edges Ec as output:
complement:= function(V, E, Ec)
begin
for u in V do
for v in V do
//gets all edges from u to v
E1[u,v]:= getEdges(u,v);
//No edge from u to v
if E1[u,v] = empty then
addEdge(Ec, (u,v,1))
else
for e in E1[u,v] do
w:= weight(e);
if w <> 1 then
e':= (e.u, e.v, inverse(w));
addEdge(Ec, e')
end
end
end
end
end
end
The graph class implements the algorithm using the getComplementGraph() method
#include <zeusmath/System/Graph.h>
TAutoPtr<TGraph> ptrGraph = new TGraph(false);
//adding vertices and edges
...
TAutoPtr<TGraph> ptrGraphC;
if (ptrGraph->getComplementGraph(ptrGraphC) == RET_NOERROR)
{
...
}
3. Usefull links to the graph theory
Following links are concerned with graph theory: